コレクション 中学 数学 確率 公式 969670-中学 数学 確��� 公式

中学数学 確率の問題を攻略できる5つのコツ Qikeru 学びを楽しくわかりやすく

中学入試の算数で出題される「場合の数」の問題の解き方を解説しています。計算を使って解く方法を解説しています。 中学受験のための算数塾 エデュサポのline公式アカウントでは、勉強を頑張1矢を的AとBにそれぞれ1本だけ発射するとき、 a b 3 が整数になる確率を求めなさい。 上のヒントでも使った図を見てみましょう！ 矢を的AとBにそれぞれ1本だけ発射するとき、Aが6通りあ

中学 数学 確率 公式

中学 数学 確率 公式-中学数学確率・場合の数の超基本！！基本問題まとめ 11,063views 14年06月17日公開;必ず起こる確率はp=1, 絶対に起こらない確率はp=0である。 確率の求め方 起こりうる場合が全部でn通りあり、どの場合が起こることも同様に確からしいとき。 あることがらがおこる場合がa通り

中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく

高校数学A確率 教科書（問題・解答・公式・解説） 学校よりわかりやすいサイト このページでは、数学A「確率」の教科書の問題と解答をまとめています。 教科書の問題は出版社によって異な中学数学 確率 確率の導入 同様に確からしい (動画のみの解説) なぜ，コインやサイコロの問題は組み合わせを使って解いてはいけないのか．組み合わせを使って確率を求めてよいのはどういうとき 確率の問題と解き方（さいころやくじなど）｜中学数学 確率の相対度数は「ある出来事がどのくらいの頻度で起きたか」を表します。 相対度数 = 起きた回数 ÷ 試行回数 さいころを投

解説 コインの出方はどのようなものがあるでしょうか。 表を 、裏を×とすると、 2 2 枚とも表 1 1 枚だけ表 × 2 2 枚とも裏 ×× よって、全場合の数は 3 3 通り、 両方表は 1 1 通り、 求める確率 今回は「 確率 」のテスト対策プリントになります。 中学2年で学習する内容です。 図や表を使って解いていきますが、使い分けができるようになること、問題で問われていることがキーワード 高校生 数学 文系数学 確率 場合の数 ツイート;

中学 数学 確率 公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	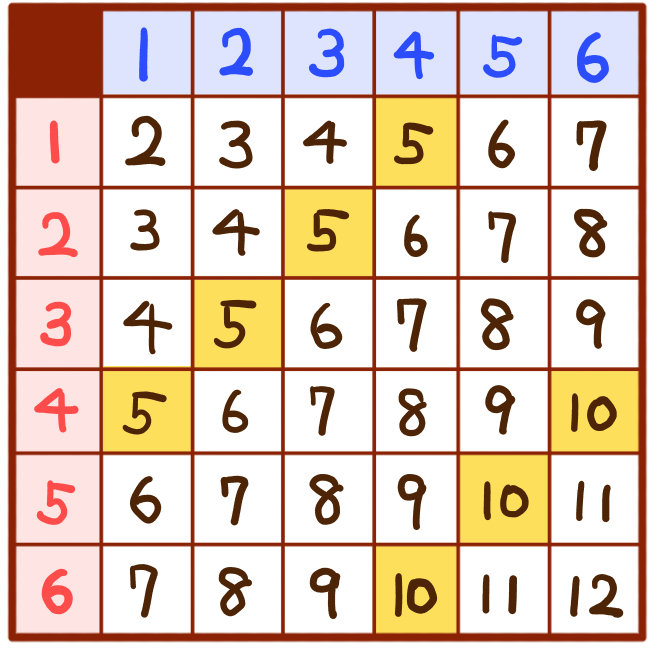順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ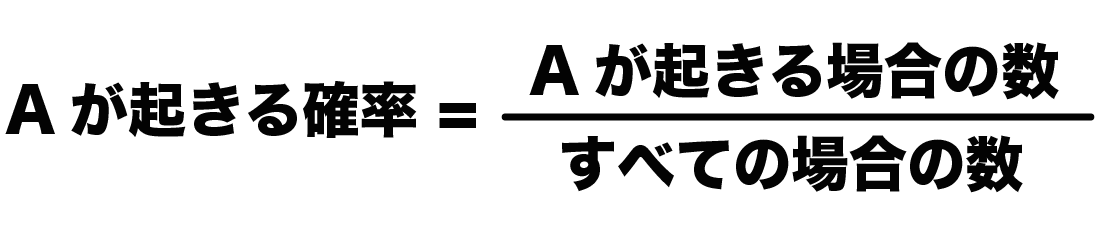
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ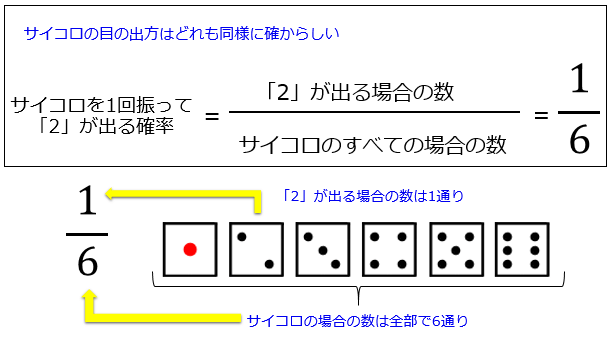
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	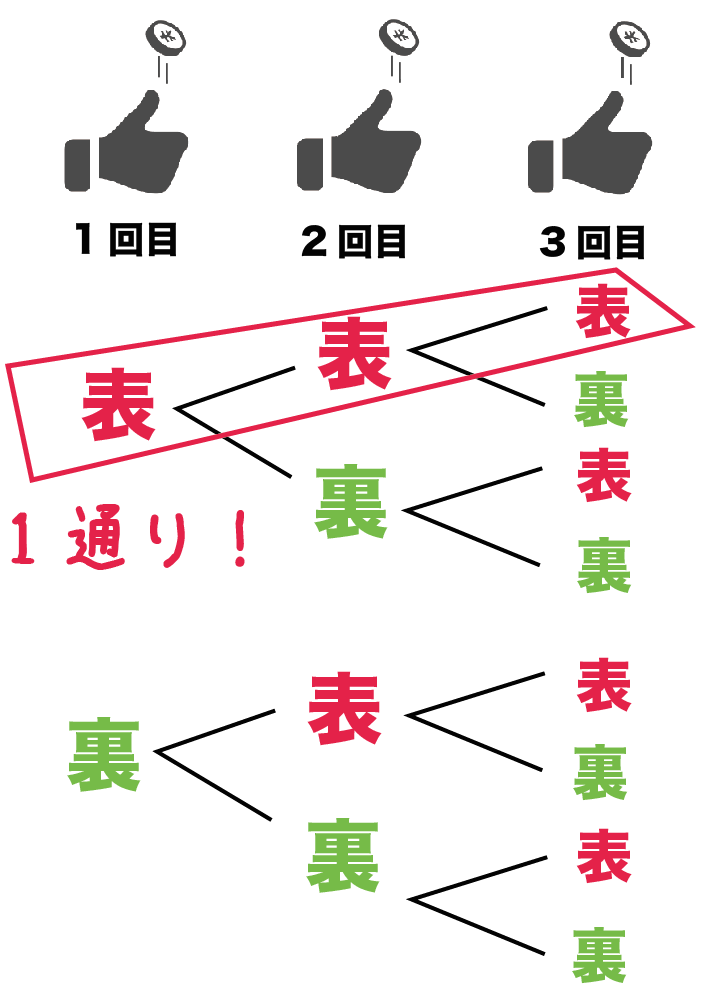順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ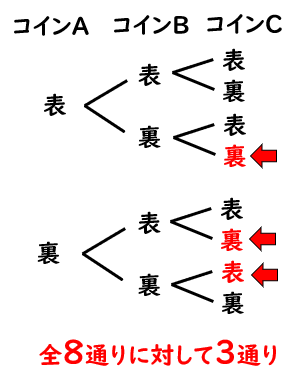
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列と組み合わせの公式とその違い 問題付き 理系ラボ	順列と組み合わせの公式とその違い 問題付き 理系ラボ

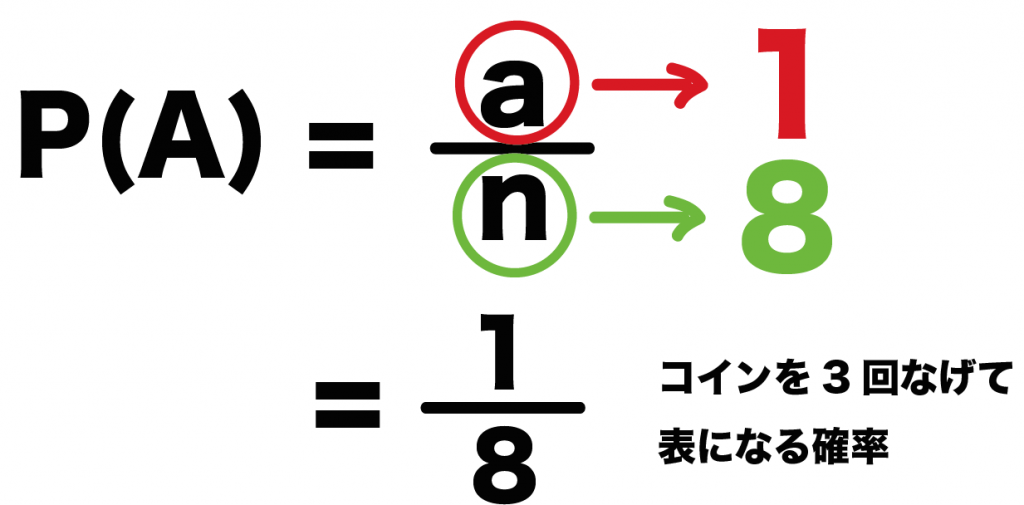
（確率）＝（それが起こる場合）/（全体） たとえば、サイコロを投げて4の目が出る場合を考えよう。 1～6の目があるから、 全体で6通り あるね。 （全体）は6。 4の目が出るのは1通りだから たった一つの公式を使って求めることができる中学の確率 中学校2年で習う確率の公式は、たったの一つです。 確率は、 $$\text{確率} = \frac{\text{ある条件が起こる場合の数}}{\text{す

Incoming Term: 中学 数学 確率 公式,